Le reti e il progresso tecnologico

L’integrale è un operatore inverso della derivata,quindi avendo una funzione y=f(x), trovare una funzione che ammetta f(x) come derivata e che quindi sarà detta primitiva di f(x).

Quindi possiamo dire che ∫f(x) dx = F(x) + C <=> F ‘ (x) = f(x)

Dunque se F(x) è una primitiva di f(x), F(x) + C è la primitiva più generale e rappresenta tutte e le sole funzioni la cui derivata è uguale a f(x).

Questa primitiva generale, costituita da una famiglia di funzioni primitive che derivate danno la funzione integranda, prendono il nome di integrale indefinito, esso viene rappresentato così:

∫f(x) dx

Proprietà dell’integrale indefinito

1) L’integrale di una costante per una funzione è uguale alla costante per l’integrale della funzione. Es. ∫k f(x) dx = k ∫f(x) dx

2) L’integrale della somma algebrica di due o più funzioni è uguale alla somma algebrica degli integrali delle singole funzioni. Es. ∫f1(x)+f2(x) dx = ∫f1(x) dx + ∫f2(x) dx

Integrali immediati

Per integrazione di una funzione si intendono le procedure di calcolo necessarie per ottenere la primitiva, se la funzione integranda e la derivata di una funzione nota, l’integrazione è immediata.

Ecco alcuni esempi di integrali immediati:

∫1/x dx = ln|x| + C                                                              ∫senx dx =-cosx dx + C

∫dx = x + C                                                                         ∫cosx dx = senx dx + C

∫xⁿ = xⁿ⁺¹/n+1 + C                                                             ∫1/cos²x dx = tg x + C

Metodi di integrazione

Quando il calcolo di un integrale risulta complesso è opportuno usare alcuni metodi che ci permettono di scriverli in un’altra forma per poi ricondurli ad integrali immediati.

I principali metodi sono:

1) Integrazione per scomposizione si applica dissociando i termini,si può aggiungere un artificio oppure nell’integrazione delle funzioni irrazionali fratte.

2) Integrazione per sostituzione avviene sostituendo alla variabile d’integrazione x una funzione di un’altra variabile t, purchè sia derivabile e invertibile.

3) Integrazione per parti si applica quando una funzione non è la derivata dell’altra la formula utilizzata è la seguente: ∫u(x)v'(x) dx = u(x)v(x) – ∫u'(x)v(x) dx

Essa è composta da u(x) detto fattore finito e da v'(x) detto fattore differenziale.

Integrale definito

L’integrale definito nasce principalmente per:

1)  Calcolo delle aree di figure delimitate da curve.

2) Calcolo di volumi.

3) Calcolo del lavoro di una forza.

Area del trapezoide

Avendo una funzione y = f(x) definita e continua nell’intervallo [a, b],vogliamo calcolare l’area della regione di piano sottesa al grafico di f(x) nell’intervallo [a, b].

Possiamo determinare l’area approssimandola con dei rettangoli inscritti e dei rettangoli circoscritti.

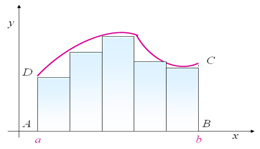Dividendo in n parti l’intervallo [a, b], avremo n rettangoli di base
h = (b – a)/n

Indichiamo con
s_n = Sommatoria area rettangoli inscritti

L’area del plurirettangolo  inscritto .

Analogamente possiamo determinare l’area  S_n  del plurirettangolo circoscritto
S_n = Sommatoria area rettangoli circoscritti, ne segue che, l’area S del trapezoide sarà sempre compresa tra sn e Sn quindi:

Sommatoria area rettangoli inscritti <=    S    <=  Sommatoria area rettangoli circoscritti

Si può concludere dicendo che:

Se y = f(x) è continua e positiva in [a, b], allora le successioni delle aree s1, s2, … sn, …  e S1, S2, …Sn,…  convergono allo stesso limite  S uguale all’area del trapezoide.